Are you desperately looking for 'stellar number coursework'? All the details can be found on this website.
Celestial body Number Coursework Complete papers are carried out by capable and proven writers whose credentials and portfolios, we testament be glad to introduce on your demand. It is 6 years already as we enforce comprehensive essay aid online for complete in need.
Table of contents
- Stellar number coursework in 2021
- Stellar number coursework 02
- Stellar number coursework 03
- Stellar number coursework 04
- Stellar number coursework 05
- Stellar number coursework 06
- Stellar number coursework 07
- Stellar number coursework 08
Stellar number coursework in 2021
 This image shows stellar number coursework.
This image shows stellar number coursework.
Stellar number coursework 02
 This picture shows Stellar number coursework 02.
This picture shows Stellar number coursework 02.
Stellar number coursework 03
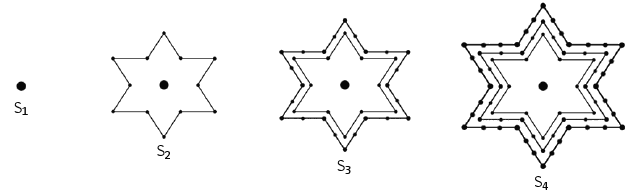 This image representes Stellar number coursework 03.
This image representes Stellar number coursework 03.
Stellar number coursework 04
 This picture demonstrates Stellar number coursework 04.
This picture demonstrates Stellar number coursework 04.
Stellar number coursework 05
 This image illustrates Stellar number coursework 05.
This image illustrates Stellar number coursework 05.
Stellar number coursework 06
 This picture representes Stellar number coursework 06.
This picture representes Stellar number coursework 06.
Stellar number coursework 07
 This picture shows Stellar number coursework 07.
This picture shows Stellar number coursework 07.
Stellar number coursework 08
 This picture demonstrates Stellar number coursework 08.
This picture demonstrates Stellar number coursework 08.
Is the number of dots inside a stellar shape always 1?
However, since the main concern for this investigation is counting the number of dots inside a “stellar” geometric shape, it must be inclusive that they form the shape of a classical star, then the limitation would be as when it is substituted into the equation the result it yields is always 1.
Which is an example of a stellar number?
Stellar numbers. The simplest examples of these numbers would square numbers 1, 4, 9, 16, which are the squares of the values 1, 2, 3 and 4 as demonstrated by this table and by the formula . Henceforth, all tables generated are from the Numbers program by the macintosh company and all mathematical notation is from the program Mathtype 6.0.
What is the formula for P stellar numbers?
In fact the p-stellar numbers will have the formula pn 2 – pn + 1. We can prove this by using the same recurrence relationship before: and by noting that the outside star edge is found in the same way as before for a p-stellar shape – only this time we subtract p for the number of vertices counted twice.
How to find the nth term for 6 stellar numbers?
Once this is done, we are asked to find the nth term for the 6-stellar numbers (with 6 vertices) below: Once again we can use the method for quadratic sequences. The second difference is 12, giving us an 2 + bn + c with a = 12/2 = 6.
Last Update: Oct 2021
Leave a reply
Comments
Latane
24.10.2021 07:18Generalising for p-stellar numbers. Stellar is one of the many applications of the blockchain technology.
Armittie
26.10.2021 00:29Nuclear reactions, the microscopical physics of astral opacity, etc. Different information recovery methods.